Moment of inertia
| Classical mechanics | ||||||||||
History of classical mechanics · Timeline of classical mechanics
|
||||||||||
- This article is about the moment of inertia of a rotating object. For the moment of inertia dealing with bending of a plane, see second moment of area.
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, or the angular mass, (SI units kg·m²) is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation. The moment of inertia plays much the same role in rotational dynamics as mass does in linear dynamics, describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities. The symbol I and sometimes J are usually used to refer to the moment of inertia or polar moment of inertia.
While a simple scalar treatment of the moment of inertia suffices for many situations, a more advanced tensor treatment allows the analysis of such complicated systems as spinning tops and gyroscopic motion.
The concept was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765.[1] In this book, he discussed the moment of inertia and many related concepts, such as the principal axis of inertia.
Contents |
Overview
The moment of inertia of an object about a given axis describes how difficult it is to change its angular motion about that axis. Therefore, it encompasses not just how much mass the object has overall, but how far each bit of mass is from the axis. The farther out the object's mass is, the more rotational inertia the object has, and the more force is required to change its rotation rate. For example, consider two hoops, A and B, made of the same material and of equal mass. Hoop A is larger in diameter but thinner than B. It requires more effort to accelerate hoop A (change its angular velocity) because its mass is distributed farther from its axis of rotation: mass that is farther out from that axis must, for a given angular velocity, move more quickly than mass closer in. So in this case, hoop A has a larger moment of inertia than hoop B.

The moment of inertia of an object can change if its shape changes. A figure skater who begins a spin with arms outstretched provides a striking example. By pulling in her arms, she reduces her moment of inertia, causing her to spin faster (by the conservation of angular momentum).
The moment of inertia has two forms, a scalar form, I, (used when the axis of rotation is specified) and a more general tensor form that does not require the axis of rotation to be specified. The scalar moment of inertia, I, (often called simply the "moment of inertia") allows a succinct analysis of many simple problems in rotational dynamics, such as objects rolling down inclines and the behavior of pulleys. For instance, while a block of any shape will slide down a frictionless decline at the same rate, rolling objects may descend at different rates, depending on their moments of inertia. A hoop will descend more slowly than a solid disk of equal mass and radius because more of its mass is located far from the axis of rotation, and thus needs to move faster if the hoop rolls at the same angular velocity. However, for (more complicated) problems in which the axis of rotation can change, the scalar treatment is inadequate, and the tensor treatment must be used (although shortcuts are possible in special situations). Examples requiring such a treatment include gyroscopes, tops, and even satellites, all objects whose alignment can change.
The moment of inertia is also called the mass moment of inertia (especially by mechanical engineers) to avoid confusion with the second moment of area, which is sometimes called the moment of inertia (especially by structural engineers). The easiest way to differentiate these quantities is through their units (kg·m² as opposed to m4). In addition, moment of inertia should not be confused with polar moment of inertia, which is a measure of an object's ability to resist torsion (twisting) only.
Scalar moment of inertia
Consider a rigid body rotating with angular velocity ω around a certain axis. The body consists of N point masses mi whose distances to the rotation axis are denoted ri. Each point mass will have the speed vi = ωri, so that the total kinetic energy T of the body can be calculated as
In this expression the quantity in parentheses is called the moment of inertia of the body (with respect to the specified axis of rotation). It is a purely geometric characteristic of the object, as it depends only on its shape and the position of the rotation axis. The moment of inertia is usually denoted with the capital letter I:
It is worth emphasizing that ri here is the distance from a point towards the axis of rotation, not towards the origin. As such, the moment of inertia will be different when considering rotations about different axes.
Similarly, the moment of inertia of a continuous solid body rotating about a known axis can be calculated by replacing the summation with the integral:
where r is the radius vector of a point within the body, ρ(r) is the mass density at point r, and d(r) is the distance from point r to the axis of rotation. The integration goes over the volume V of the body.
Properties
The moment of inertia of the body is additive. That is, if a body can be decomposed (either physically or conceptually) into several constituent parts, then the moment of inertia of the whole body about a given axis is equal to the sum of moments of inertia of each part around the same axis.[2]
Examples
Diatomic molecule, with atoms m1 and m2 at a distance d from each other, rotating around the axis which passes through the molecule’s center of mass and is perpendicular to the direction of the molecule.
The easiest way to calculate this molecule’s moment of inertia is to use the parallel axis theorem. If we consider rotation around the axis passing through the atom m1, then the moment of inertia will be I1 = m1·0 + m2·d 2 = m2d 2. On the other hand, by the parallel axis theorem this moment is equal to I1 = I + (m1 + m2)·a2, where I is the moment of inertia around the axis passing through the center of mass, and a is the distance between the center of mass and the first atom. By the center of mass formula, this distance is equal to a = m2d / (m1 + m2). Thus,
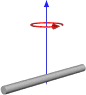
Thin rod of mass m and length ℓ, rotating around the axis which passes through its center and is perpendicular to the rod.
Let Oz be the axis of rotation, and Ox the axis along the rod. If ρ is the density, and s the cross-section of the rod (so that m = ρℓs), then the volume element for the integral formula will be equal to dV = s·dx, where x changes from −½ℓ to ½ℓ. The moment of inertia can be found by computing the integral:
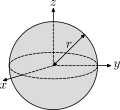
Solid ball of mass m and radius R, rotating around an axis which passes through the center.
Suppose Oz is the axis of rotation. The distance from point r = (x,y,z) towards the axis Oz is equal to d(r)2 = x2 + y2. Thus, in order to compute the moment of inertia Iz, we need to evaluate the integral ∭(x2 + y2) dV. The calculation considerably simplifies if we notice that by symmetry of the problem, the moments of inertia around all axes are equal: Ix = Iy = Iz. Then
where r2 = x2 + y2 + z2 is the distance from point r to the origin. This integral is easy to evaluate in the spherical coordinates, the volume element will be equal to dV = 4πr2dr, where r goes from 0 to R. Thus,
Composite Bodies
Based on dimensional analysis alone, the moment of inertia of a non-point object must take the form:
where
- M is the mass
- L is a length dimension taken from the centre of mass (in some cases, the length of the object is used instead.)
- c is a dimensionless constant called the inertial constant that varies with the object in consideration.
Inertial constants are used to account for the differences in the placement of the mass from the center of rotation. Examples include:
- c = 1, thin ring or thin-walled cylinder around its center,
- c = 2/5, solid sphere around its center
- c = 1/2, solid cylinder or disk around its center.
When c is 1, the length (L) is called the radius of gyration.
Parallel axis theorem
Once the moment of inertia has been calculated for rotations about the center of mass of a rigid body, one can conveniently recalculate the moment of inertia for all parallel rotation axes as well, without having to resort to the formal definition. If the axis of rotation is displaced by a distance  from the center of mass axis of rotation (e.g., spinning a disc about a point on its periphery, rather than through its center,) the displaced and center-moment of inertia are related as follows:
from the center of mass axis of rotation (e.g., spinning a disc about a point on its periphery, rather than through its center,) the displaced and center-moment of inertia are related as follows:
This theorem is also known as the parallel axes rule and is a special case of Steiner's parallel-axis theorem.
Equations involving the moment of inertia
The rotational kinetic energy of a rigid body can be expressed in terms of its moment of inertia. For a system with  point masses
point masses 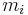 moving with speeds
moving with speeds 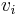 , the rotational kinetic energy
, the rotational kinetic energy  equals
equals
where  is the common angular velocity (in radians per second). The final expression I ω2 / 2 also holds for a mass density function with a generalization of the above derivation from a discrete summation to an integration.
is the common angular velocity (in radians per second). The final expression I ω2 / 2 also holds for a mass density function with a generalization of the above derivation from a discrete summation to an integration.
In the special case where the angular momentum vector is parallel to the angular velocity vector, one can relate them by the equation
where L is the angular momentum and  is the angular velocity. However, this equation does not hold in many cases of interest, such as the torque-free precession of a rotating object, although its more general tensor form is always correct.
is the angular velocity. However, this equation does not hold in many cases of interest, such as the torque-free precession of a rotating object, although its more general tensor form is always correct.
When the moment of inertia is constant, one can also relate the torque on an object and its angular acceleration in a similar equation:
where 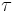 is the torque and
is the torque and 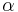 is the angular acceleration.
is the angular acceleration.
Moment of inertia tensor
In three dimensions, if the axis of rotation is not given, we need to be able to generalize the scalar moment of inertia to a quantity that allows us to compute a moment of inertia about arbitrary axes. This quantity is known as the moment of inertia tensor and can be represented as a symmetric positive semi-definite matrix, I. This representation elegantly generalizes the scalar case: The angular momentum vector, is related to the rotation velocity vector, ω by
and the kinetic energy is given by
as compared with
in the scalar case.
Like the scalar moment of inertia, the moment of inertia tensor may be calculated with respect to any point in space, but for practical purposes, the center of mass is almost always used.
Definition
For a rigid object of  point masses
point masses 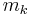 , the moment of inertia tensor is given by
, the moment of inertia tensor is given by
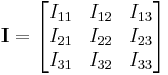 ,
,
where
and 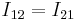 ,
, 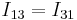 , and
, and 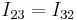 . (Thus
. (Thus 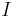 is a symmetric tensor.)
is a symmetric tensor.)
Here 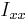 denotes the moment of inertia around the
denotes the moment of inertia around the 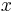 -axis when the objects are rotated around the x-axis,
-axis when the objects are rotated around the x-axis, 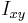 denotes the moment of inertia around the
denotes the moment of inertia around the 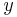 -axis when the objects are rotated around the
-axis when the objects are rotated around the 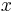 -axis, and so on.
-axis, and so on.
These quantities can be generalized to an object with distributed mass, described by a mass density function, in a similar fashion to the scalar moment of inertia. One then has
where  is their outer product, E3 is the 3 × 3 identity matrix, and V is a region of space completely containing the object. Alternatively, the equation above can be represented in a component-based method. Recognizing that, in the above expression, the scalars
is their outer product, E3 is the 3 × 3 identity matrix, and V is a region of space completely containing the object. Alternatively, the equation above can be represented in a component-based method. Recognizing that, in the above expression, the scalars 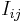 with
with 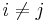 are called the products of inertia, a generalized form of the products of inertia can be given as
are called the products of inertia, a generalized form of the products of inertia can be given as
The diagonal elements of 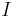 are called the principal moments of inertia.
are called the principal moments of inertia.
Derivation of the tensor components
The distance  of a particle at
of a particle at 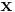 from the axis of rotation passing through the origin in the
from the axis of rotation passing through the origin in the 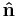 direction is
direction is 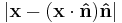 . By using the formula
. By using the formula 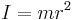 (and some simple vector algebra) it can be seen that the moment of inertia of this particle (about the axis of rotation passing through the origin in the
(and some simple vector algebra) it can be seen that the moment of inertia of this particle (about the axis of rotation passing through the origin in the 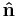 direction) is
direction) is 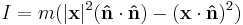 This is a quadratic form in
This is a quadratic form in 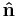 and, after a bit more algebra, this leads to a tensor formula for the moment of inertia
and, after a bit more algebra, this leads to a tensor formula for the moment of inertia
![{I} = m [n_1,n_2,n_3]\begin{bmatrix}
y^2+z^2 & -xy & -xz \\
-y x & x^2+z^2 & -yz \\
-zx & -zy & x^2+y^2
\end{bmatrix} \begin{bmatrix}
n_1 \\
n_2\\
n_3
\end{bmatrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/dacd5f0fa6ccbb3553e0d656e4a58b2f.png) .
.
This is exactly the formula given below for the moment of inertia in the case of a single particle. For multiple particles we need only recall that the moment of inertia is additive in order to see that this formula is correct.
Reduction to scalar
For any axis 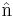 , represented as a column vector with elements ni, the scalar form I can be calculated from the tensor form I as
, represented as a column vector with elements ni, the scalar form I can be calculated from the tensor form I as
The range of both summations correspond to the three Cartesian coordinates.
The following equivalent expression avoids the use of transposed vectors which are not supported in maths libraries because internally vectors and their transpose are stored as the same linear array,
However it should be noted that although this equation is mathematically equivalent to the equation above for any matrix, inertia tensors are symmetrical. This means that it can be further simplified to:
Principal axes of inertia
By the spectral theorem, since the moment of inertia tensor is real and symmetric, it is possible to find a Cartesian coordinate system in which it is diagonal, having the form
where the coordinate axes are called the principal axes and the constants 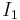 ,
, 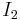 and
and 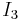 are called the principal moments of inertia. The principal axes of a body, therefore, are a cartesian coordinate system whose origin is located at the center of mass. [3] The unit vectors along the principal axes are usually denoted as (e1, e2, e3). This result was first shown by J. J. Sylvester (1852), and is a form of Sylvester's law of inertia. The principal axis with the highest moment of inertia is sometimes called the figure axis or axis of figure.
are called the principal moments of inertia. The principal axes of a body, therefore, are a cartesian coordinate system whose origin is located at the center of mass. [3] The unit vectors along the principal axes are usually denoted as (e1, e2, e3). This result was first shown by J. J. Sylvester (1852), and is a form of Sylvester's law of inertia. The principal axis with the highest moment of inertia is sometimes called the figure axis or axis of figure.
When all principal moments of inertia are distinct, the principal axes are uniquely specified. If two principal moments are the same, the rigid body is called a symmetrical top and there is no unique choice for the two corresponding principal axes. If all three principal moments are the same, the rigid body is called a spherical top (although it need not be spherical) and any axis can be considered a principal axis, meaning that the moment of inertia is the same about any axis.
The principal axes are often aligned with the object's symmetry axes. If a rigid body has an axis of symmetry of order  , i.e., is symmetrical under rotations of 360°/m about a given axis, the symmetry axis is a principal axis. When
, i.e., is symmetrical under rotations of 360°/m about a given axis, the symmetry axis is a principal axis. When 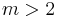 , the rigid body is a symmetrical top. If a rigid body has at least two symmetry axes that are not parallel or perpendicular to each other, it is a spherical top, e.g., a cube or any other Platonic solid.
, the rigid body is a symmetrical top. If a rigid body has at least two symmetry axes that are not parallel or perpendicular to each other, it is a spherical top, e.g., a cube or any other Platonic solid.
The motion of vehicles is often described about these axes with the rotations called yaw, pitch, and roll.
A practical example of this mathematical phenomenon is the routine automotive task of balancing a tire, which basically means adjusting the distribution of mass of a car wheel such that its principal axis of inertia is aligned with the axle so the wheel does not wobble.
Parallel axis theorem
Once the moment of inertia tensor has been calculated for rotations about the center of mass of the rigid body, there is a useful labor-saving method to compute the tensor for rotations offset from the center of mass.
If the axis of rotation is displaced by a vector R from the center of mass, the new moment of inertia tensor equals
where m is the total mass of the rigid body, E3 is the 3 × 3 identity matrix, and  is the outer product.
is the outer product.
Rotational symmetry
Using the above equation to express all moments of inertia in terms of integrals of variables either along or perpendicular to the axis of symmetry usually simplifies the calculation of these moments considerably.
Comparison with covariance matrix
The moment of inertia tensor about the center of mass of a 3 dimensional rigid body is related to the covariance matrix of a trivariate random vector whose probability density function is proportional to the pointwise density of the rigid body by:
where n is the number of points.
The structure of the moment-of-inertia tensor comes from the fact that it is to be used as a bilinear form on rotation vectors in the form
Each element of mass has a kinetic energy of
The velocity of each element of mass is 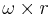 where r is a vector from the center of rotation to that element of mass. The cross product can be converted to matrix multiplication so that
where r is a vector from the center of rotation to that element of mass. The cross product can be converted to matrix multiplication so that
and similarly
Thus,
plugging in the definition of ![[\cdot]_\times](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/13500ce53c18a4912d92f5e3a9d88281.png) the
the ![[r]_\times^\top [r]_\times](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9116002cef17aefae446be4ce3f317a3.png) term leads directly to the structure of the moment tensor.
term leads directly to the structure of the moment tensor.
See also
- List of moments of inertia
- List of moment of inertia tensors
- Rotational energy
- Parallel axis theorem
- Perpendicular axis theorem
- Stretch rule
- Tire balance
- Poinsot's ellipsoid
- Instant centre of rotation
Notes
- ↑ Euler, Leonhard (1765-01-01) (in Latin), Theoria motus corporum solidorum seu rigidorum: Ex primis nostrae cognitionis principiis stabilita et ad omnes motus, qui in huiusmodi corpora cadere possunt, accommodata, Cornell University Library, ISBN 978-1429742818
- ↑ “Mass moment of inertia” by Mehrdad Negahban, University of Nebraska
- ↑ Blake, Alexander (1985), Handbook of mechanics, materials, and structures, Wiley-IEEE, ISBN 0471862398, http://books.google.com/?id=Wp1XC3mN_2IC&pg=PA202&dq=%22principal+axis%22+moment+of+inertia+maximum
References
- Goldstein, H. (1980), Classical Mechanics (2nd ed.), Addison-Wesley, ISBN 0-201-02918-9.
- Landau, LD; Lifshitz (1976), Mechanics (3rd ed.), Pergamon Press, ISBN 0-08-021022-8 (hardcover); ISBN 0-08-029141-4 (softcover).
- Marion, JB; Thornton, ST. (1995), Classical Dynamics of Systems and Particles (4th ed.), Thomson, ISBN 0-03-097302-3.
- Sylvester, J J (1852), "A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares", Philosophical Magazine IV: 138–142, http://www.maths.ed.ac.uk/~aar/sylv/inertia.pdf, retrieved 2008-06-27
- Symon, KR (1971), Mechanics (3rd ed.), Addison-Wesley, ISBN 0-201-07392-7.
- Tenenbaum, RA (2004), Fundamentals of Applied Dynamics, Springer, ISBN 0-387-00887-X.
External links
- Angular momentum and rigid-body rotation in two and three dimensions
- Lecture notes on rigid-body rotation and moments of inertia
- The moment of inertia tensor
- An introductory lesson on moment of inertia: keeping a vertical pole not falling down (Java simulation)
- Tutorial on finding moments of inertia, with problems and solutions on various basic shapes
- Measuring moment of inertia
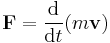
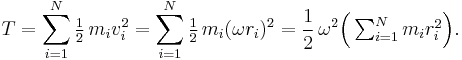
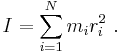
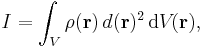
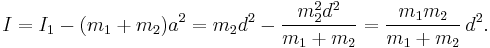
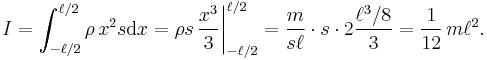
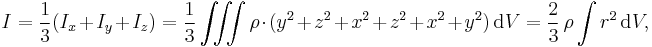
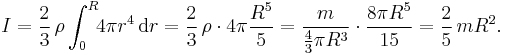
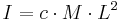
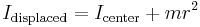
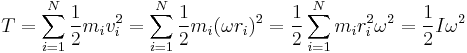
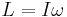
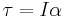
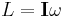
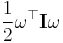
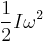
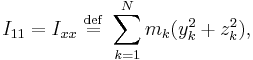
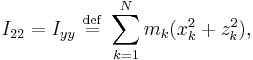
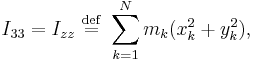
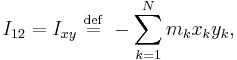
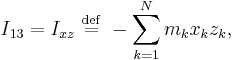
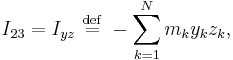
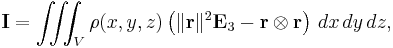
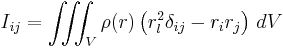
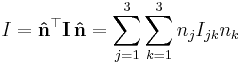
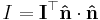
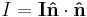
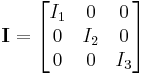
![\mathbf{I}^{\mathrm{displaced}} = \mathbf{I}^{\mathrm{center}} + m \left[ \left(\mathbf{R} \cdot \mathbf{R}\right) \mathbf{E}_{3} - \mathbf{R} \otimes \mathbf{R} \right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5685f05491ff00428551ec8ad91b5de0.png)
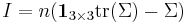
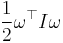
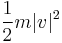
![\omega\times r = [r]_\times^\top \omega\,\!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/094bf7983509e9ef849a52534a1e5ee6.png)
![(\omega\times r)^\top = ([r]_\times \omega)^\top = \omega^\top [r]_\times^\top \,\!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8d51101272f20bcd01f2a96e337296ca.png)
![|v|^2 = (\omega\times r)^\top(\omega\times r)=\omega^\top [r]_\times^\top [r]_\times \omega \,\!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/815aafeec20d88b72a01c19a50ad055e.png)